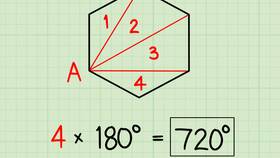
В геометрии смежные углы - это два угла, которые имеют общую вершину и общую сторону, а их несовпадающие стороны образуют прямую линию. Сумма смежных углов является важной характеристикой, которая часто используется при решении геометрических задач.
Содержание
Основное свойство смежных углов
| Свойство | Значение |
| Сумма смежных углов | Всегда равна 180° (развернутому углу) |
Доказательство свойства
Рассмотрим два смежных угла ∠AOB и ∠BOC:
- Общая сторона OB делит развернутый угол ∠AOC на два угла
- По определению, градусная мера развернутого угла равна 180°
- Следовательно, ∠AOB + ∠BOC = ∠AOC = 180°
Практическое применение свойства
Примеры использования в задачах
| Тип задачи | Применение свойства |
| Нахождение неизвестного угла | Если один из смежных углов известен, второй находится вычитанием из 180° |
| Доказательство параллельности прямых | Используется при доказательстве теорем о параллельных прямых |
| Построение перпендикулярных линий | Позволяет определить прямой угол (90°) |
Пример решения задачи
Дано: ∠ABC = 125°. Найти смежный с ним угол.
- Обозначим смежный угол как ∠CBD
- По свойству смежных углов: ∠ABC + ∠CBD = 180°
- 125° + ∠CBD = 180°
- ∠CBD = 180° - 125° = 55°
Дополнительные свойства смежных углов
- Если один из смежных углов прямой (90°), то второй также будет прямым
- Биссектрисы двух смежных углов перпендикулярны друг другу
- Смежные углы всегда дополняют друг друга до развернутого угла
Отличие смежных углов от вертикальных
| Характеристика | Смежные углы | Вертикальные углы |
| Сумма углов | 180° | Равны между собой |
| Расположение | Имеют общую сторону | Нет общей стороны |
Историческая справка
Понятие смежных углов и их свойств было известно еще древнегреческим математикам. Евклид в своих "Началах" (III век до н.э.) использовал свойства смежных углов при доказательстве различных геометрических теорем. Это фундаментальное свойство лежит в основе многих разделов геометрии.
Знание о том, что сумма смежных углов равна 180°, является базовым для изучения более сложных геометрических концепций и широко применяется в архитектуре, инженерии и других практических областях.