Сумма векторов - это вектор, полученный в результате операции сложения двух или более векторов. Векторное сложение подчиняется определенным математическим правилам и имеет важное значение в физике, инженерии и компьютерной графике.
Содержание
Основные методы сложения векторов
| Метод | Описание | Формула |
| Правило треугольника | Конец первого вектора соединяется с началом второго | AB + BC = AC |
| Правило параллелограмма | Векторы откладываются от общей точки | a + b = c (диагональ параллелограмма) |
| Координатный метод | Сложение соответствующих координат | (x₁+x₂, y₁+y₂, z₁+z₂) |
Свойства суммы векторов
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Наличие нулевого вектора: a + 0 = a
- Наличие противоположного вектора: a + (-a) = 0
Примеры сложения векторов
- Сложение сил в физике (равнодействующая сила)
- Определение результирующей скорости
- Расчет перемещения тела
- Композиция движений в механике
Геометрическая интерпретация
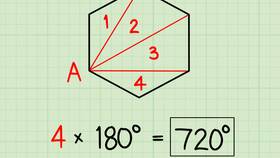
Геометрически сумма векторов представляет собой замыкающую векторную цепочку. Для двух векторов она равна диагонали параллелограмма, построенного на этих векторах. При сложении нескольких векторов используется правило многоугольника - каждый последующий вектор откладывается от конца предыдущего.
Особые случаи
При сложении коллинеарных векторов (лежащих на одной прямой) их модули либо складываются (если направления совпадают), либо вычитаются (если направления противоположны). Сумма перпендикулярных векторов вычисляется по теореме Пифагора.